Ad Disclosure
RADIO WARS: The Ratings
By Kyle Scott
Published:

The latest Nielsen ratings are out for the “Holiday Period” running December 3 to December 30. Here’s how the local sports talk radio battle shakes out, and some additional information with regard to streaming numbers. All estimates are based on men 25-54:
6 a.m. – 10 a.m.
Angelo Cataldi and Co. on WIP earned an 8.3 over-the-air and a 0.2 on the stream, for a combined total of 8.5. Anthony Gargano and friends on 97.5 earned a 6.5 over-the-air and 1.1 on the stream, for a combined total of 7.6.
10 a.m. – 2 p.m.
Mike and Ike on WIP earned a 6.3 over-the-air and a 0.5 on the stream, for a combined total of 6.8. Harry and Rob on 97.5 are in the mix, they earned a 4.8 over-the-air and a 2.0 over the stream, for a combined total of 6.8.
2 p.m. – 6 p.m.
And in the main event, Mike Missanelli earned a 6.7 over-the-air and a 1.6 on the stream, for a combined total of 8.3. Josh Innes and compadres earned a 6.1 over-the-air and a 0.3 on the stream, for a combined total of 6.4.
…
Few things to call out as it pertains to Missanelli-Innes: This is the second-straight month Missanelli has won over-the-air, after losing to Innes, over-the-air, most of last year. Missanelli’s over-the-air lead increased from 0.3 points last month to 0.6 points this month. In fact, Missanelli’s over-the-air number beat Innes’ OTA-stream combined number– 6.7 to 6.4. So no matter how you shake it or spin it, Missanelli won last month, and increased his lead doing so.
…
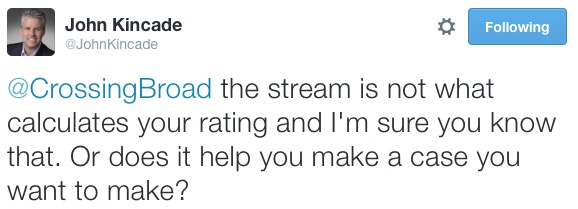
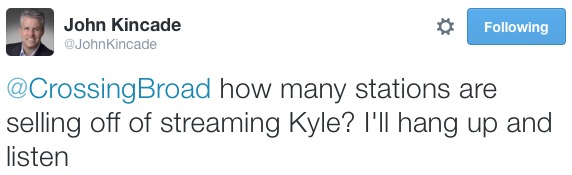
There’s been a lot of contention surrounding the inclusion of streaming estimates, which Nielsen measures from the same sample group as over-the-air numbers but doesn’t officially recognize combination of the two, which, as you can see in our little bloviatory skirmish, works in 97.5’s favor. It makes sense, however, to combine them, especially since you’re comparing apples to apples (0.1 is worth the same OTA as it is on the stream). Josh Innes thinks I’m a biased asshole for doing it this way, presumably because, a few months ago, he cold-called me out of the blue to give me his winning over-the-air number and then got upset when I obtained the full report, included the stream, and declared Mike the winner. We, um, discussed it earlier this month:
Longtime sports talk radio man and Philly guy John Kincade, currently in Atlanta, chimed in on that conversation and backed Nielsen’s currently antiquated refusal to acknowledge the combination of both numbers:
OK, I’ll respond to the caller’s question. Two things:
- I’m hearing that stations are actually seeing higher numbers (compared to estimates) on the hard listener data available to them for the stream. In some cases, much higher. It goes to show just how wrong estimates can be, regardless of listening device. But it also shows that including the stream is a very necessary thing to do in 2016, given how many people choose to listen that way.
- Also hearing that, maybe as early as the spring, Nielsen will begin “total line reporting”– either officially blessing stations to combine their OTA and stream number for advertising (or dick-measuring) purposes, or combine the two into one overall number for purposes of ranking stations. [Currently, the OTA and stream numbers are broken out on separate line items, advertising is sold off only the OTA number, and hosts are bonused off only the OTA number.]
So, despite gripes from the likes of Innes and Kincade, it seems Nielsen will finally step into the decade and begin combing OTA and stream numbers, which, for Innes, and WIP overall, probably won’t be a good thing. MY MUSIC OH SO LOUD:

Kyle Scott is the founder and editor of CrossingBroad.com. He has written for CBS Philly and Philly Voice, and been a panelist or contributor on NBC Sports Philly, FOX 29 and SNY TV, as well as a recurring guest on 97.5 The Fanatic, 94 WIP, 106.7 The Fan and other stations. He has more than 10 years experience running digital media properties and in online advertising and marketing.